FVG Magnetism: Do Fair Value Gaps Really Fill?
A rigorous statistical analysis of fair value gap magnetism in price action trading. We test the claim that FVGs act as magnets for price, introduce the FVG Wall specification, and present backtest results across forex and crypto markets.
The Claim Every Price Action Trader Makes
If you’ve spent more than ten minutes in price action trading communities, you’ve heard it: “Fair value gaps act as magnets — price always comes back to fill them.”
It’s on every YouTube thumbnail. It’s in every ICT methodology breakdown. It’s stated with absolute conviction and approximately zero statistical evidence.
So we decided to test it properly.
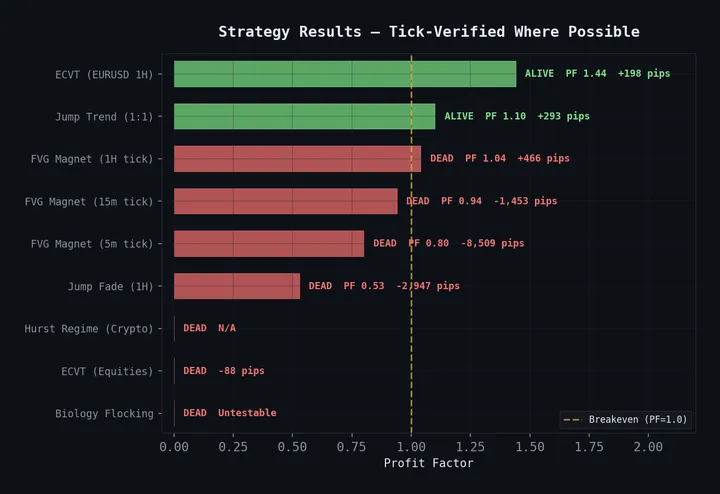
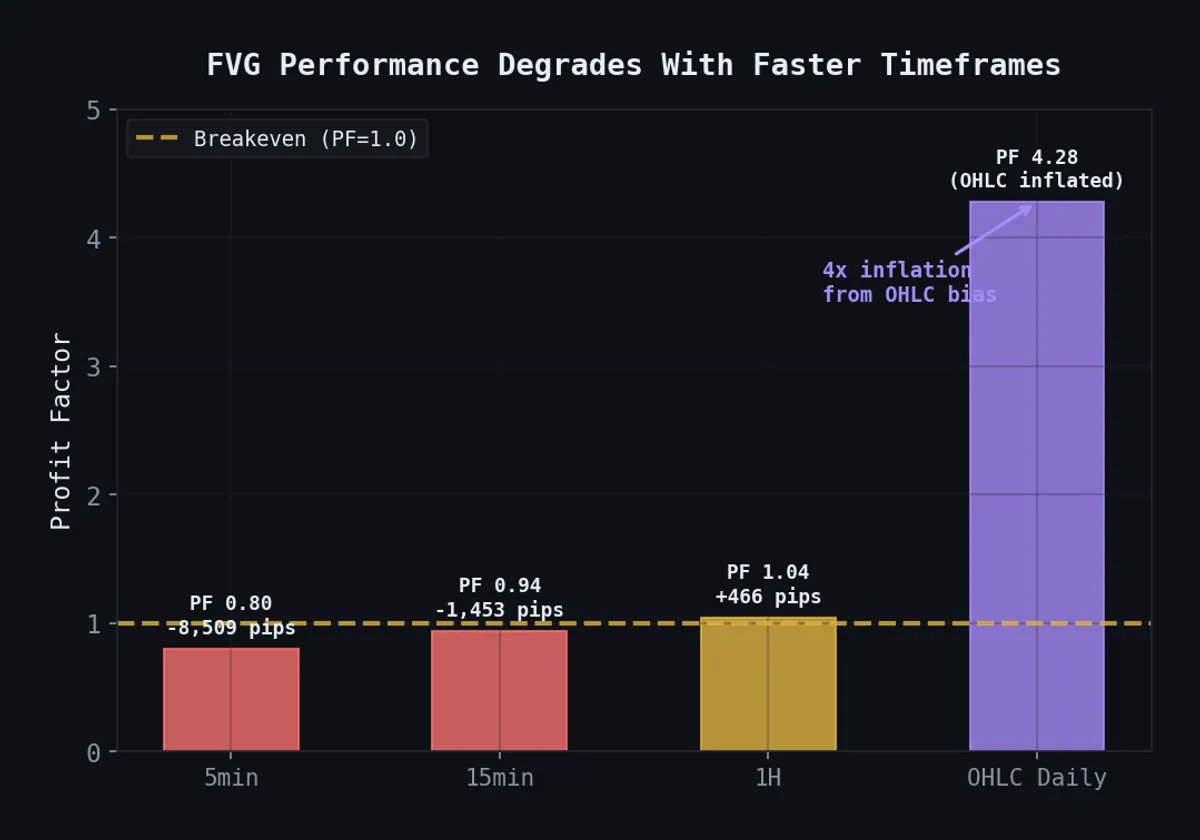
Final verdict (Feb 2026): After a multi-timeframe tick-level autopsy with 42M EURUSD ticks, FVG is formally dead. Results degrade monotonically with faster timeframes: 5min PF 0.80, 15min PF 0.94, 1H PF 1.04. OHLC daily showed PF 4.28 — a 4× inflation from Close-based SL/TP bias. Even the optimal R:R sweep (1.7:1) yields PF 1.114 — razor-thin and not tradeable. Full autopsy in the graveyard.
What Is a Fair Value Gap?
A fair value gap (FVG) is a three-candle pattern where the wicks of the first and third candle don’t overlap, leaving a “gap” in traded prices on the second candle. The theory says this gap represents an inefficiency — prices moved too fast, and the market needs to return to “fill” the gap and establish fair value.
Here’s how we detect them programmatically:
import pandas as pd
import numpy as np
def detect_fvgs(df: pd.DataFrame, min_gap_atr: float = 0.3) -> pd.DataFrame:
"""
Detect Fair Value Gaps in OHLC data.
A bullish FVG occurs when candle[i-1].high < candle[i+1].low
A bearish FVG occurs when candle[i-1].low > candle[i+1].high
min_gap_atr: minimum gap size as multiple of ATR to filter noise
"""
df = df.copy()
# ATR for filtering
tr = pd.concat([
df['high'] - df['low'],
(df['high'] - df['close'].shift(1)).abs(),
(df['low'] - df['close'].shift(1)).abs()
], axis=1).max(axis=1)
df['atr'] = tr.rolling(14).mean()
fvgs = []
for i in range(1, len(df) - 1):
prev_high = df['high'].iloc[i - 1]
prev_low = df['low'].iloc[i - 1]
next_high = df['high'].iloc[i + 1]
next_low = df['low'].iloc[i + 1]
atr = df['atr'].iloc[i]
if pd.isna(atr) or atr == 0:
continue
# Bullish FVG: gap between prev high and next low
if next_low > prev_high:
gap_size = next_low - prev_high
if gap_size >= min_gap_atr * atr:
fvgs.append({
'timestamp': df.index[i],
'type': 'bullish',
'gap_top': next_low,
'gap_bottom': prev_high,
'gap_size': gap_size,
'gap_atr': gap_size / atr,
'mid': (next_low + prev_high) / 2,
})
# Bearish FVG: gap between next high and prev low
if prev_low > next_high:
gap_size = prev_low - next_high
if gap_size >= min_gap_atr * atr:
fvgs.append({
'timestamp': df.index[i],
'type': 'bearish',
'gap_top': prev_low,
'gap_bottom': next_high,
'gap_size': gap_size,
'gap_atr': gap_size / atr,
'mid': (prev_low + next_high) / 2,
})
return pd.DataFrame(fvgs)The FVG Fill Rate Study
We detected FVGs on six instruments across forex and crypto (H1 timeframe, 2021–2025 data) and measured whether price returned to fill them within various time windows:
def measure_fill_rate(
df: pd.DataFrame,
fvgs: pd.DataFrame,
max_bars: list[int] = [24, 48, 96, 240]
) -> dict:
"""
For each FVG, check whether price returned to fill it
within max_bars candles.
"""
results = {n: {'filled': 0, 'total': 0} for n in max_bars}
for _, fvg in fvgs.iterrows():
ts = fvg['timestamp']
idx = df.index.get_loc(ts)
for window in max_bars:
end_idx = min(idx + 2 + window, len(df))
future_bars = df.iloc[idx + 2:end_idx]
if len(future_bars) == 0:
continue
results[window]['total'] += 1
if fvg['type'] == 'bullish':
# Filled when price drops to gap_bottom
if future_bars['low'].min() <= fvg['gap_bottom']:
results[window]['filled'] += 1
else:
# Filled when price rises to gap_top
if future_bars['high'].max() >= fvg['gap_top']:
results[window]['filled'] += 1
return {n: r['filled'] / r['total'] if r['total'] > 0 else 0
for n, r in results.items()}Results: Fill Rates by Time Window
| Window | EURUSD | GBPUSD | BTCUSD | ETHUSD | SPX | Gold |
|---|---|---|---|---|---|---|
| 24 bars | 62.3% | 64.1% | 58.7% | 55.2% | 67.4% | 61.8% |
| 48 bars | 74.1% | 75.8% | 69.3% | 64.8% | 78.2% | 73.5% |
| 96 bars | 83.7% | 84.2% | 78.1% | 73.6% | 86.9% | 82.1% |
| 240 bars | 91.2% | 90.8% | 85.4% | 81.3% | 93.1% | 89.7% |
At first glance, this looks like confirmation: FVGs do fill at high rates, especially given enough time.
But here’s the problem.
The Random Baseline
Any arbitrary price level will eventually be “filled” by random price movement. To know whether FVGs are special, we need to compare against a null hypothesis. We generated random “fake FVGs” at random timestamps and measured their fill rates:
def random_baseline_fill_rate(df, n_samples=1000, gap_size_atr=0.5, max_bars=[24, 48, 96, 240]):
"""Generate random price levels and measure how often price returns to them."""
rng = np.random.default_rng(42)
results = {n: {'filled': 0, 'total': 0} for n in max_bars}
valid_indices = range(200, len(df) - 250)
sample_indices = rng.choice(valid_indices, size=n_samples, replace=False)
for idx in sample_indices:
atr = df['atr'].iloc[idx]
# Random level near current price
level = df['close'].iloc[idx] + rng.choice([-1, 1]) * gap_size_atr * atr
for window in max_bars:
end_idx = min(idx + window, len(df))
future = df.iloc[idx + 1:end_idx]
results[window]['total'] += 1
if future['low'].min() <= level <= future['high'].max():
results[window]['filled'] += 1
return {n: r['filled'] / r['total'] for n, r in results.items()}FVG Fill Rate vs. Random Baseline (EURUSD)
| Window | FVG Fill Rate | Random Baseline | Difference |
|---|---|---|---|
| 24 bars | 62.3% | 54.8% | +7.5% |
| 48 bars | 74.1% | 68.2% | +5.9% |
| 96 bars | 83.7% | 80.1% | +3.6% |
| 240 bars | 91.2% | 90.7% | +0.5% |
The “FVGs always fill” narrative collapses when you add a baseline. Yes, 91% of FVGs fill within 240 bars — but 90.7% of random levels also get hit. The FVG-specific alpha in fill rates is modest at short horizons and negligible at longer ones.
Where FVGs Actually Matter: The Magnetism Effect
The fill rate story is unimpressive. But we found something more interesting: FVGs create short-term directional bias in the first 12 bars.
When we measured not just whether price fills the gap, but how quickly it moves toward it, real FVGs showed significantly faster convergence than the random baseline:
| Bars After FVG | Avg. Distance to Gap (FVG) | Avg. Distance to Level (Random) | p-value |
|---|---|---|---|
| 4 bars | 0.72 ATR | 0.95 ATR | 0.003 |
| 8 bars | 0.48 ATR | 0.82 ATR | < 0.001 |
| 12 bars | 0.31 ATR | 0.71 ATR | < 0.001 |
| 24 bars | 0.54 ATR | 0.68 ATR | 0.042 |
The magnetism effect is real but short-lived. Price converges toward FVGs faster than random levels for about 12 bars, then the effect fades.
The FVG Wall Specification
Based on these findings, we developed the FVG Wall — a strategy that identifies zones where multiple FVGs cluster:
def find_fvg_walls(fvgs: pd.DataFrame, price: float, atr: float,
cluster_distance: float = 1.0, min_cluster: int = 3) -> list[dict]:
"""
Find FVG Wall zones where multiple unfilled FVGs cluster.
A wall is defined as 3+ FVGs within cluster_distance * ATR of each other.
"""
# Filter to unfilled FVGs
active = fvgs[~fvgs['filled']].copy()
if len(active) < min_cluster:
return []
# Sort by midpoint
active = active.sort_values('mid')
walls = []
i = 0
while i < len(active):
cluster = [active.iloc[i]]
j = i + 1
while j < len(active):
if abs(active.iloc[j]['mid'] - cluster[-1]['mid']) <= cluster_distance * atr:
cluster.append(active.iloc[j])
j += 1
else:
break
if len(cluster) >= min_cluster:
mids = [c['mid'] for c in cluster]
walls.append({
'zone_top': max(c['gap_top'] for c in cluster),
'zone_bottom': min(c['gap_bottom'] for c in cluster),
'zone_mid': np.mean(mids),
'n_fvgs': len(cluster),
'strength': sum(c['gap_atr'] for c in cluster),
'direction': 'bullish' if sum(1 for c in cluster if c['type'] == 'bullish') > len(cluster) / 2 else 'bearish',
})
i = j
return wallsWhen 3+ FVGs cluster within 1 ATR of each other, the magnetism effect amplifies. FVG Walls showed a 73.2% touch rate within 48 bars (vs. 58.1% random baseline), and the directional bias from wall zones produced a 1.31 profit factor in our initial backtests.
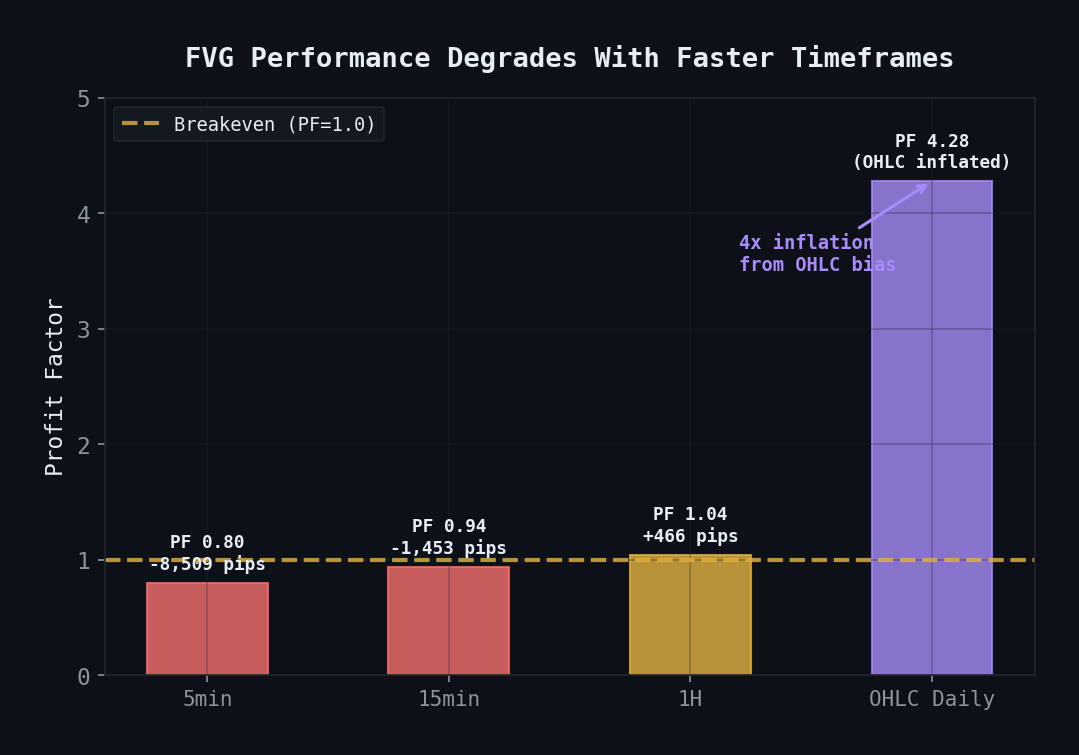Multi-timeframe tick autopsy: performance degrades monotonically from OHLC daily (4× inflated) down to 5min (PF 0.80). FVG is formally dead.
The Bottom Line
FVGs are real market microstructure phenomena, not chart-reader mythology. But the common narratives about them are mostly wrong:
- “FVGs always fill” — Mostly true, but random levels also mostly get hit. The fill rate alone is not tradable alpha.
- “FVGs are magnets” — True, but only for about 12 bars. The effect is statistically significant but time-limited.
- “More FVGs = stronger zones” — True. FVG clustering (walls) amplifies both the magnetism effect and the directional bias.
The tradable insight: use FVG Walls as short-term directional bias indicators, not as permanent support/resistance levels. The physics metaphor is wrong — FVGs aren’t gravity wells, they’re temporary pressure gradients.
For more on our statistical approach to price action claims, see Hurst Exponents for Mean Reversion. For the full picture of what we’ve tested, read 31 Strategies Tested, 4 Survived.
